Elastic beam deflection calculator example

Consider a 13-meter steel cantilever beam (a beam attached to a wall that doesn't allow for any deflection on that side), anchored on the right, has a downward load of 100 Newtons applied to it 7 meters from the left end. How far down will the left end of the beam bend?

The first step is to determine the value of Young's Modulus to be used; since the beam is made of steel, we go with the given steel value: 206,850 MPa, which is 206,850,000,000 Pa (remember, since everything else is in metric and using N/m/s, we use single Pascals).

Next, determine the moment of inertia for the beam; this usually is a value given in most textbook problems, or if it needs to be calculated, a listing of formulas for determining moment of inertias for many common geometries is provided here. *Note: this application uses the Area Moments of Inertia, which are listed first.
For this example, we're just going to say that the beam is square and has a crossection side length of 0.5m. So...

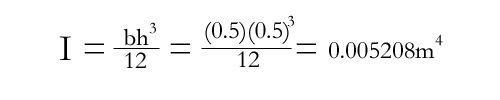
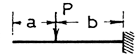
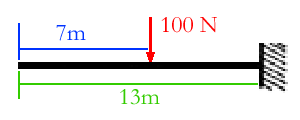
This is a good time to choose the loading case, so looking over the list, it looks like loading case #13 is our best bet; its beam is cantilevered on one end, and it has the single point load that is not a set distance from either end.

After checking the load-case button, enter in the rest of the values as they are given: a point load equal to 100 Newtons, total beam length is 13 meters, no applied moments or distributed loads, partial length "a" is 7 meteres, partial length "b" is the remaining 6 meters, and voila! ready to see just how far this beam gets bent. Click on the "Submit For Calculation" button to see the results.

Young's modulus (E) :
Values of Young's Modulus

Moment of inertia (I):	Total length (L):
Partial length (a):	Partial length (b):

Point load (P):
Uniform distributed load (q):
Applied moment (M₀) :
Applied moment (M₁):	Applied moment (M₂) :

Right End Slope (θ_r) =
Left End Slope (θ_l)=
Maximum Deflection (y) =

Elastic beam deflection calculator example

Loading Cases