Page 1 of 2
kquad and csbend
Posted: 15 Mar 2013, 14:24
by eliana
If I understand correctly declaring a quadrupole as a kquad (or a bending magnet as csbend) with n_kicks=10 is equivalent to split the quad (or bend) in 10 slices.
The user must pay attention that n_kicks is large enough for correctly reproducing the optics. Is it correct?
Re: kquad and csbend
Posted: 15 Mar 2013, 18:07
by michael_borland
Eliana,
The "n_kicks" parameter is misnamed. It should have been called "n_steps". For integration_order=2 (not recommended, but the only option in the early days), they are the same. For integration_order=4 (default, recommended), the actual number of kicks applied is 3*n_kicks, because a fourth-order integrator is used.
Yes, the value is at the discretion of the user. For short elements or elements in which the lattice functions are nearly constant, it can be smaller. For ring tracking, I would typically use N_KICKS=24 for quads, but it has to be determined for each lattice.
--Michael
Re: kquad and csbend
Posted: 16 Sep 2014, 04:46
by libov
Michael,
how does one determine suitable N_KICKS for some particular lattice?
Please have a look at two attached lattices. they are exactly the same except that one is using QUAD and the other KQUAD elements to model quadrupoles.
If I use default N_KICKS=4, tracking results (emittance evolution or bunch length evolution) are very much different between the two.
However, setting N_KICKS to a larger number, say N_KICKS=24, gives almost perfect match between the two. Is it an indicator that the value is sufficient?
And can you please briefly explain what happens that KQUAD gives so different results for different N_KICKS ?
(or please refer me to some reference on this kick method of quadrupole description ... )
Thanks a lot!
Slava
Re: kquad and csbend
Posted: 16 Sep 2014, 08:55
by michael_borland
Slava,
The QUAD element is implemented as a matrix, up to 3rd order. The matrix is built from solutions that are exact, at least to the given order. First-order properties, such as tunes and beta functions, are exact. However, beyond the first order solution the element is not symplectic and so is generally not appropriate for tracking in rings.
The KQUAD element is implemented using a 2nd or 4th order symplectic integrator and so is suited for tracking with rings. However, although it is always symplectic, it isn't always accurate. That depends on the N_KICKS setting (really should be called N_SLICES). The more kicks, the smaller the numerical integration step size and the greater the accuracy. For the default fourth-order integrator, the error scales like 1/N_KICKS^5. The integrator is described in E. Forest, AIP Conf. Proc. 184, 1106-1136; see section 2.
The necessary value of N_KICKS will depend on many things, such as the strength and length of the quadrupole and the beta function at the quadrupole. I usually vary N_KICKS until the tunes match the expected values to ~0.001. Usually 20-40 is suitable. If I really need to optimize running time, I vary N_KICKS for each quadrupole family separately until I see only small changes in the tunes.
--Michael
Re: kquad and csbend
Posted: 12 Oct 2016, 11:41
by zhilong
michael_borland wrote:Eliana,
Hi Michael,
When I set the parameters n_kicks for kquad and csband, ksext, the tune will be all the same when n_kicks vary by 4,10,20,or 100. I think maybe the twiss output file make no effects on the n_kicks. But how to set the *.ele file to make n_kicks effective? I have change the parameters in twiss output one by one, but make no sense.
Thank you very much
--Zhilong Pan
Re: kquad and csbend
Posted: 12 Oct 2016, 11:41
by zhilong
Hi Michael,
When I set the parameters n_kicks for kquad and csband, ksext, the tune will be all the same when n_kicks vary by 4,10,20,or 100. I think maybe the twiss output file make no effects on the n_kicks. But how to set the *.ele file to make n_kicks effective? I have change the parameters in twiss output one by one, but make no sense.
Thank you very much
--Zhilong Pan[/quote]
Re: kquad and csbend
Posted: 12 Oct 2016, 20:46
by michael_borland
Zhilong,
When I set the parameters n_kicks for kquad and csband, ksext, the tune will be all the same when n_kicks vary by 4,10,20,or 100. I think maybe the twiss output file make no effects on the n_kicks. But how to set the *.ele file to make n_kicks effective? I have change the parameters in twiss output one by one, but make no sense.
That's correct. The N_KICKS parameters don't make any difference in the twiss_output results. The Twiss parameters are computed using matrices, not from tracking. If you want to see the tunes change with the N_KICKS parameter, you should use the tune_footprint command or map_analysis command.
--Michael
Re: kquad and csbend
Posted: 20 Aug 2018, 06:40
by Akhyani
Dear Michael and all,
In order to find the instability thresholds in longitudinal/transverse ring tracking, which definition of dipole (CSBEN, SBEND), quadrupole (QUAD, KQUAD) and sextupole (SEXT, KSEXT) is more accurate?
Using (KQUAD,KSEXT,CSBEN) takes a long time to run, but I wasn't sure if I change these to QUAD and SEXT, the results will be reliable or not. What do you recommend?
Best,
Mina
Re: kquad and csbend
Posted: 20 Aug 2018, 08:30
by michael_borland
Mina,
Typically for this type of tracking we use the ILMATRIX element to replace the ring. It is much, much faster than element-by-element tracking and appears quite accurate. To verify this, a few test runs can be done using CSBEND, KQUAD, and KSEXT.
You can find a few examples of setting up ILMATRIX in the on-line examples file, e.g., multibunchCollectiveEffects/ILMatrixFromTracking.
--Michael
Re: kquad and csbend
Posted: 10 Sep 2018, 08:25
by Akhyani
Dear Michael,
Thanks for your recommendation. I built ILMATRIX element for our lattice through the online example provided in the website. For test, I took 7000 turn tracking for both ILMATRIX and (CSBEN,KQUAD & KSEXT). I was supposed to get the same results from both trackings but no similarity appeared, as can be seen in the pictures below:
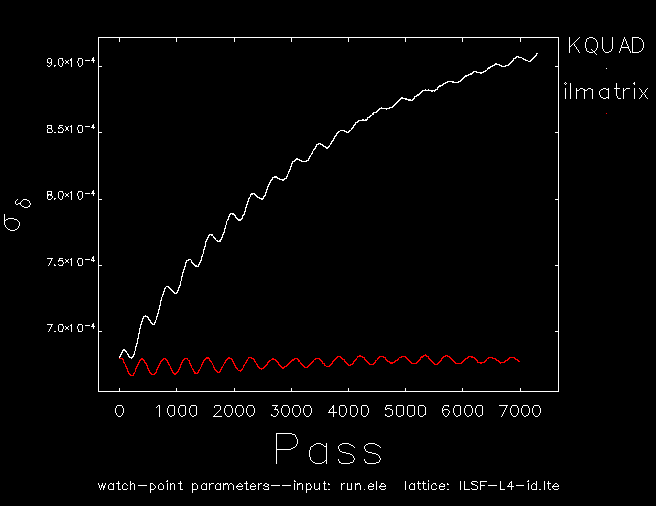
- energySpread.png (6.8 KiB) Viewed 14896 times
I was wondering if you could help me to resolve this issue. The lattice is attached.
with many thanks,
Mina